|
|
The Elijah Laboratories Logo |
|
R. J. Brown Elijah Laboratories Inc.
The Faceted Annulus The logo of Elijah Laboratories Inc. is more than just a simple geometric symbol. 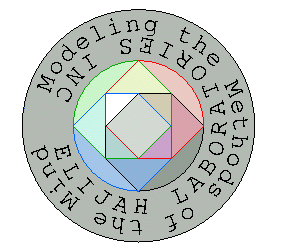 Fig 1. The Faceted Annulus Logo of Elijah Laboratories Inc. It is rooted in the geometry of the inner workings of the mind, and is based on a mathematical proof that describes the operation of the human nerve cell — the fundamental building block of our brains. It may be described visually as a "faceted annulus", since the outer ring with the phrases "Modelling the Methods of the Mind" and "Elijah Laboratories Inc." is an annulus:
And the inner dircle is "faceted" with multi-colored facets:
The inscriptions "Elijah Laboratories Inc." and "Modelling the Methods of the Mind" are self-explanatory. It is the multi-colored faceted inner circle and the grey annular region that surrounds it that I will will now explain. The Perceptron Incompleteness TheoremIn the mid 1960's, work by Nills J. Nillsen and others on automatic pattern recognition laid the foundation for what later came to be called "artificial neural networks". This work was based on the abstract mathematical model of the biological neuron, or nerve cell, developed by McCullough and Pitts in the late 1940's. The McCullough-Pitts Neuron is basically nothing more than a Bayesian classifier. Bayesian classifiers are of renewed importance on the internet today, as some of the most effective spam filters are bayesian classifiers. This enables them to adapt to the changing techniques employed by spammers because they can learn, while they operate, how to recognize new patterns that indicate that an email is spam. Rosenblatt et al developed an algorithm for automatically adjusting the sensitivities of the inputs to this neuron model so that it could be automatically "trained" to recognize [almost] any desired pattern. More properly, it was trained to discriminate between 2 pattern sets, outputting one symbol if the input was classified as in the first set, and another symbol if it was classified in the second set. The 2 sets were disjoint, and their union formed the universe of discourse. Additional work by Nillsen et al developed configurations of multiple such neurons into neural networks that were capable of recognizing more complex distinctions among multiple patterns. In particular, a 2-layer network, called the Committee Network, was fairly successful at being trained to recognize a wide variety of patterns. Nonetheless, sometimes — with certain pattern sets — the training algorithm failed to converge; it would continually adjust the weights, but never find an adjustment that worked for all the patterns in the training set:
It was eventually proved (mathematically) that such a model of the neuron was fundamentally incomplete. This is known as The Perceptron Incompleteness Theorem (and also as the XOR problem), and is a famous result of artificial neural network theory. In the early 1970's, research into Artificial Intelligence, or AI, was divided into two camps: the "messy", and the "neat". The "neat" group was involved with automated reasoning and deduction, also known as automatic theorem proving, and the "messy" crowd was doing artificial neural network research. Research money for AI was primarily from defense funding, and was fairly limited. The two camps competed with each other for this money. Marvin Minsky published a book in the early 1970's that condemned the neural approach because of the incompleteness theorem. He claimed that this theorem proved that the neural approach was fundamentally flawed, and that research money should be directed at the symbolic reasoning approach suppoprted by the neats. This book was instrumental in directing funding away from artificial neural nertworks and towards the symbolic reasoning approach instead. But Minsky's conclusion that neural networks were fundamentally flawed was based on the assumption that since the simple McCullough-Pitts neuron building block, also known as a Perceptron, or Threshold Logic Unit (TLU), was flawed, then therefore one could not build a more complex structure using only those building blocks that was not likewise flawed. Minsky was wrong! In the early 1980's, several neural network architectures were developed, most notably the Back Propagation Network, that used a sigmoid neural activation function instead of a threshold activation function, and were more than 2 layers deep. Mathematical proofs exist that show that these networks are not limited by the perceptron incompleteness theorem. In 1975, Mr. Robert J. Brown, the founder of Elijah Laboratories Inc., became involved in neural network research. By 1976, he was actively working on a committee network pattern classifier, written in FORTRAN, and running on a PDP-11/05 minicomputer. In 1977, he had a working classifier. This program worked in spite of the fact that it had a serious bug in the training algorithm. In 1981, this research was continued, this time in BASIC on a Hewlett-Packard microcomputer using an 8085 and the CP/M operating system. The bug was discovered and fixed at that time, resulting in much faster training. In 1983, this work was submitted for publication, but was not actually published until 1987, after the program had been translaterd into the C programming language. It was published as An Artificial Neural Network Experiment, and was the cover article on the April issue of Dr. Dobb's Journal in 1987. As part of this work, Mr. Brown developed a new geometric proof of the perceptron incompleteness theorem. This result was presented at the 1987 Rochester Forth Conference, and published in the proceedings as Committee Networks: What They Can and Cannot Do. It is the geometry of this proof that is the inspiration for the the faceted annulus logo of Elijah Laboratories Inc. The Geometry of the ProofAs pointed out in the proof, the perceptron incompleteness theorem can be reduced to the problem of discriminating between all possible 2-input binary switching functions. This amounts to 4 combinations of 2 inputs, and 16 different ways to dichotomize them; therefore, we will need a way to recognize 16 different regions in this space if we are to be successful in training the TLU to recognize all possible such switching functions. The geometry of a TLU implements a hyperplane as the representation of a pattern with the positive and negative sides of the plane corresponding to the 2 regions being dichotomized. The current state of training of a TLU is represented by a point, called a weight point in the space that contains the pattern plane. In the 2-input switching function case, the possible inputs correspond to 4 pattern planes, one for each possible combination of the 2 binary inputs. It is a property of the pattern planes that they all must pass thru the origin of the weight space. So we have 4 2-dimensional Euclidean geometrical planes, all passing through the origin of a 3-dimensional Euclidean space. It is shown in the proof that this divides the space into only 14 regions. This is demonstrated by showing that there exists an isomorphism between the regions in the space that the planes and the sphere inhabit and the regions into which the surface of the sphere is divided by the intersection of those planes with the surface of the sphere as great circles, or geodesics . We thereby achieve a reduction of dimension , or a reduction of basis , mapping a 3D problem onto a 2D geometry, without loss of generality. The only way we can get the required 16 regions is by including not only the 14 2-D regions on the surface of the sphere, but also the 3-D region inside the sphere as one additional region, and the 3-D region outside the sphere as the other missing region. Since these two additional regions lie outside the dimensional restrictions of the original problem, they are not reachable by the problem as we have constructed it. More about this later... If, instead of working with the 2 dimensional Riemannian surface of the sphere, we were dealing with the same topological map only on the surface of a torus, then we could obtain the required additional intersection regions, as the torus is topologically richer in connectedness than the sphere, but this author does not see any way to make sense out of using a toroidal surfacce in the required context. When we examine this reduced basis representation, we see that there are 4 regions topologicaly equivalent to circles that intersect like a Venn diagram in the resulting polar projection of the surface of the sphere onto the following planar map: 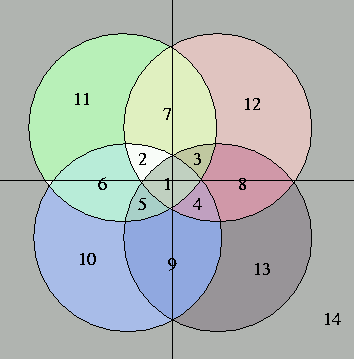 Fig 2. The Projection of the Geodesics onto the Plane. The 14 distinct regions into which this space is divided are numbered in the above map, and colored to correspond to the original colors in the faceted annulus logo of Fig 1. Each of the circles in the above map is a projection of one of the great circles resulting from the intersection of the original pattern places with the surface of the sphere. Furthermore, it can be seen that each such circle intersects all the other circles in all possible combinations except for the following 2 cases: circle 11 cannot intersect circle 13 without simultaneously intersecting at least one of the other circles (10 and 12), and likewise, circles 10 and 12 cannot intersect each other without simultaneously intersecting at least one of circles 11 and 13. We may therefore conclude that these two cases, corresponding to the exclusive-OR and exclusive-NOR switching functions, can never be recognized by a single TLU, no matter how it is trained. Correspondence between the Map and the LogoThe colors permit easy visualization between the above map and the original faceted annulus logo. The 4 geodesics are colored red, green, blue, and black, going counterclockwise from the first to the fourth quadrant. When these colors are mixed, according to the rules for additive colors, as in mixing colors of light, the colors of the intersecting regions are produced, with the black reducing the luminance of any region it intersects.
To further emphasize the topological equivalence between the two, consider that each of the 4 circles (outlined as 4 hexagons in the colors: red, green, blue, and black in the logo above), which were originally geodesics on the sphere, and thus the spherical equivalent of a straight line in that curved space, intersects each of the other circles in 2 places, which are geometric points. If we consider that a triangle has 3 points as vertices, and that a square has 4, then we can see that both the map and the faceted annulus contain 6 squares (regions 1, 6, 7, 8, 9, and 14) and 8 triangles (regions 2, 3, 4, 5, 10, 11, 12, and 13). These regions in the faceted annulus are colored the same, and have the same number of "points" (as intersection between great circles) as their counterparts in the map. The gray outer region (14) in Fig 2 above has its corresponding region as the logo the outer annular ring. In the projection, this region extends to infinity; in the logo, the outer bounding circle of the annulus represents the point at infinity of the polar projection. The CuboctahedronNow that we understand that the surface of the sphere is divided into 14 distinct regions — 6 squares and 8 triangles — by the pattern planes, we must ask ourselves the question, "Is there any well studied polytope, or 3-dimensional regular solid that may be inscribed in a sphere, that likewise has 6 squares and 8 triangles in the same relationship to each other as the relationship that we have derived by studying the behavior of the perceptron model of a nerve cell?" The answer is a resounding yes! It is the cuboctahedron:  Fig 3. Animation of a Cuboctahedron. It may be easily seen that the cuboctahedron also has 4 planes that pass through its center, and map to hexagons where they intersect the surface of the cuboctahedron. These correspond to the 4 planes that intersect the sphere as great circles. Another solid, the Johnson solid J27, or triangular orthobicupola, also has the required number of triangles and squares, but lacks the 4 geodesics, having only a single plane of symetry, and thus a single geodesic:
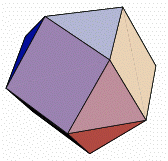 Fig 4. The Johnson solid J27, or triangular orthobicupola. Whereas the cuboctahedron has each square edge-incident with 4 triangles, and each triangle edge-incident with 3 squares, the triangular orthobicupola has each square edge-incident with 3 triangles and 1 square, annd each triangle edge-incident with 2 squares and 1 triangle. J27 may therefore be viewed as a twisted cuboctahedron. When I originally developed the geometric proof of the perceptron incompleteness theorem, I was unaware of the correspondence between the resulting geometry and the cuboctahedron. That only leaped out at me around the year 2000. I then discovered the work of R. Buckminster Fuller in his Synergetics, and also the elaborations thereupon by Iona Miller in her work The Diamond Body: Buckminster Fuller and The Qabala. One particularly interesting fact about the cuboctahedron is that it is the solution to the sphere kissing problem in 3 dimensions:  Fig 5. The 3 Dimensional Solution to the Sphere Kissing Problem. This problem asks how many peripheral unit spheres may be placed in simultaneous contact with a central unit sphere. It makes sense to ask this question about any number of dimensions, but suprisingly, the answer is only known for a few isolated cases. The answer, when known, has relevence, among other things, to the construction of certain families of error correcting codes. It is also a recurrent theme in crystalography, as variations on assemblies of cuboctahedra describe certain densest packing arrangements of crystaline solid matter. The paper Dynamical partitions of space in any dimension, p 12, by Tomaso Aste, states that the answer to the sphere kissing problem is definately known only for the following cases:
Fig 6. All Known Solutions to the Kissing Spheres Problem. This is a very active research area right now, and knowledge is accumulating quickly. A more recent source gives the following additional information:
If one connects the centers of the peripheral spheres in the solution to the 3-D sphere kissing problem, one obtains a cuboctahedron. Higher dimensional polytopes derived from the sphere kissing problem — higher dimensional analogues to the cuboctahedron — have implications in the quantuum electrodynamical study of gravity and zero point energy, or the energetic vacuum, as well as in algebraic coding theory. Metaphysical and Theological Implications Long before Euclid and other classical Greek philosophers began the systematic mathematical study of geometry, the Jewish Torah, in the book of Genesis, records that Abraham had 2 sons: Ishmael and Isaac. Most Jews and Christians are familiar with the twelve sons of Jacob, and the twelve tribes of Israel. Note that Levi was not counted in the tribes around the Tabernacle, as the Levites were the priests inside the Tabernacle; however, Joseph was not counted among the tribes either, but his two sons were, making up the total of twelve tribes of Israel — the other name for Jacob, Isaac's son — but how many realize that Ishmael also had 12 sons? Ishmael was the father of the people that now make up the religion of Islam — the other group that lays a claim on the Holy Land and the Temple Mount. The ancestral history of these two warring parties goes back to a couple of brothers, each claiming the inheritance. Now consider that the 12 tribes of Israel were instructed by Jehovah through Moses to construct a tabernacle that was to be the dwellingplace of God, and that the 12 tribes were to encamp around it in a very specific manner. Given that all this occurred in the physical realm, and represented a static relationship, we can then undestand that the dimensionality of the situation must be 3; if the situation were dynamic — time varying — then it would be 4. We have no known exact solution for the 4-D sphere kissing problem, but we know the answer in 3-D is 12. There are 12 spheres incident to a central sphere, just like there are 12 tribes surrounding the tabernacle. Twelve is the maximum number that can be in continuous contact with the center. Today we have the Temple Mount in Jerusalem, with the Dome of the Rock, a Muslim shrine, sitting directly on top of the original and future site of the Temple of Solomon, the counerpart to the Tabernacle.
 Fig 7. The Dome of the Rock on Temple Mount. We have the descendents of two fighting brothers, each fathered by the 12 children or grandchildren of each of the original two brothers, the sons of Abraham, and each claiming the promise of the inheritance originally given to Abraham by God. The Jewish and Christian scriptures have prophecies that predict the rebuilding of the Temple of Solomon. Right now, the site for that Temple is under Muslim control. A mystic offshoot of Judaism, the Qabalah, is concerned with reaching the merkabah, or throne of God. In the Qabalah, a geometrical construction known as the Tree of Life is employed as a device used in meditation. Iona Miller shows how this Tree of Life is a subset of a 2-dimensional projection of the edges of the cuboctahedron, together with the radial links to the central sphere. Further exposition regarding the relationships between the Jewish and Islamic heritage, the Qaabalah, Temple Mount, and the prophesied world leader, the Antichrist, may be found in the paper " The Number of a Man". During the Medieval Period, the practice of the Qabalah was extended by a number of non-Jewish individuals who frequently held positions as sorcerrers to Medieval rulers. They were said to have reached altered states of conciousness by this practice, in which they had dreams and vision that enabled them to predict future events. Today, we would call this either astral projection, or more colloquially, time travel. Many researchers into Zero Point Energy and the energetic vacuum predict that a thorough understanding of the physics of these things will indeed make time travel possible. Such dreams and visions also play a significant part in Judaism and Christianity. In Christianity, we have Jesus hand picking twelve men, the disciples, eleven of whom later became the twelve apostles, with Paul replacing Judas (or Matthias replacing him, depending on how you interpret what an apostle is). These disciples surrounded Jesus for 3½ years. Jesus was "the image of God." An image is a projection. The parallels to the Tabernacle and the Temple, as well as to the Tree of Life of the Qabalah, are astounding! In addition, the Temple of Solomon, and especially its construction, directed by Hiram, are central to the doctrines of Freemasonry. The founding fathers of the United States were all Masons, as have been almost all of its presidents. We also have the cultural predominance of the number 12 as the measure called a dozen, and the number 13, which includes the central sphere in the count, as the baker's dozen. We also have the 12 months in a year, and the division of the zodiac into the 12 astrological signs. Jacob's wife, Rachel, stole her fathers "images". These "images" were more than likely scientific instruments used in astrology to measure and predict the alignment of stars and planets, not mere gold statues. Astrology originated in Babylon. I do not believe that it is an accident that these particular numbers were chosen, although it is hard to trace the origins of this custom. The ubiquity cannot be coincidental. Referring back to the ealier comment that we could obtain the missing 2 regions if there were only some way to include not only the surface of the sphere, but also the 3 dimensional region inside the sphere, and the 3 dimensional region outside of it: in the light of the above metaphysical explorations, this would correspond to taking the problem outside of the physical realm and into a higher dimension: possibly the spiritual realm — from the physical plane to the spiritual plane. This interpretation also maps well onto the idea of heaven and hell, with one being at the "center of the earth", and the other being in the "heavens", with ourselves as humans living our life out on the surface of the earth. While we have been making analogy to the central sphere, and hence the center region, as being likened unto God, topology tells us that we may envert the sphere without any loss of generality, and thus put that same God, in our model, in the heavens instead of in the center of the earth. In the flat projection, this corresponds to whether we place God above, or below, the flat plane. So who is in charge here: God or Satan? Based on this model alone, you cannot really tell the difference, although you can tell that they are in opposite directions. Given that the static physical world can be represented in a 3 dimensional geometry, and that the addition of time adds another dimension, giving a total of 4, consider now the idea of 8 dimensions, as that is the next larger number for which we have definite and exact results concerning the solution to the sphere kissing problem. I propose that 8 dimensions can be interpreted as the 4 physical dimensions that we live our physical lives in, and a parallel world in the spiritual realm, where everything physical has a spiritual counterpart. Physists refer to this as the many-worlds interpretation. (See also Bell's Theorem.) Is there any significance to the number 240 that is the number of spheres incident to the central sphere in 8 dimensions? Can we find this number 240 in any literature, especially an holy scriptures of any of the world's major religions? Aside from the interpretation of 3 parallel 8 dimensional entities as described in the preceding paragraph, is there any significance that can be attached to the number 24 as the dimensionality of a metaphysical system? And is there any significance in the holy literature to the number 196560? The 3 parallel 8 dimensional universes could be viewed as a majority logic error correcting scheme to keep the universe from being perturbed by errors of individual components. Modern physics is now exploring hyperdimensional aspects of the universe, On p 6 of Saul-Paul Sirag's paper, he makes a case that the universe may have 24 vibrational degrees of freedom, and that these vibrational degrees of freedom are isomorphic to the Golay-24 code of information theory, which is much more robust than a simple majority logic error corrector. The universe, God's creation, may be self-correcting. There just ain't no way this could occur as an accident! (Fig. 8)  Fig. 8. The great cosmological accident. The nature of man and the nature of God are different. While the study of the fundamental building block of the mind of man has led us to consider the geometric properties of the cuboctahedron, we need to remember that there is also another 3-dimensional polytope that also fulfills the requirement of 8 triangular faces and 6 square faces -- the triangular orthobicupola. The primary difference between the 2 polytopes are that while the cuboctahedron exhibits radial symetry about its center, the triangular orthobicupola exhibits radial symetry about a single axis, and planar symetry about only a single plane -- the plane containing the hexagon that is normal to that single axis about which the cuboctahedron was rotated 60 degrees to result in the triangular orthobicupola. Thus the cuboctahedron has 4 geodesics, while the triangular orthobicupola has only one, which by analogy with a planet, we may call its "equator". Another interesting property possesed by the triangular orthobicupola, and not by the cuboctahedron, is that the triangular orthobicupola is a space filling polyhedron. This means that it is able to tessellate the space that contains it. An appropriate arrangement, or packing, of triangular orthobicupolae will completely fill a 3-dimensional Euclidean space, leaving no volume unfilled. Now God fills all of space; he is omnipresent. Furthermore, God is one. While the triangular orthobicupola has only a single geodesic, its equator, the cuboctahedron has four geodesics. This singular equatorial geodesic of the triangular orthobicupola, or equivalently, its axis that is normal to the equatorial plane, corresponds to that one singular God. The cuboctahedron's four geodesics correspond to man and the three contrived false Gods of the so called Holy Trinity that has been the official doctrine of the Holy Roman Catholic Church since its official inception in 325 AD at the Council of Nicea. The universe exists because God created it before he created man. Thus the universe does not need man to exist, but man certainly does need the universe to exist, at least during his physical lifetime. The unbiblical doctrine of a trinity -- God in three persons -- is a fantasy of man's conciet. In that fantasy, man is an essential part of the universe, and occupies the equatorial plane and its associated axis. It is as though the world is centered around man, and the Earth spins on man's axis. This causes man's view of God to be split into three seperate and distinct persons. In reality, this is not the case. The universe is centered on God. So we may conclude that it would be more proper to say that a cuboctahedron is a twisted triangular orthobicupola rather than the other way around, as the triune implications of a cuboctahedral geometry are a twisted representation of the truth associated with the singular geometry of the triangular orthobicupolan geometry. The presence of 3-dimensional polytopes has been experimentally observed in assocation with the gravitational field of the planet Earth. It has also been observed that these polytopes are aligned with the axis of the Earth's rotation, and are assumed to be an artifact of that rotation together with the presence of the gravitational field associated with the planet. It will require additional observations to fully elucidate the nature of the geometrical structure of these polytopes, but it is this author's expectation that they will be more akin to the triangular orthobicupola than to the cuboctahedron, as the gravitational field fills space. Thus thru gravity we may see a complete and correct space filling image of God, whereas in mind of man we can see only an imcomplete and therefore incorrect non-space filling image of God. I believe the space filling picture to be the more acurate representation. The trinitarian view of the godhead is an artifact of the way our minds are constructed, not the way the universe is constructed. Conclusion So starting with an investigation into the behavior of a simple mathematical model of a single nerve cell, and of the artificial neural networks that can be constructed with such cells, we have possibly gained some insight into one aspect of the very low level implementation of the human brain. We have also explored other situations where the same sort of geometrical construct arises, both in nature, and in the beliefs, religions, and philosophies of men. Given that the 3 dimensional geometry of the cuboctahedron arises naturally out of the assumptions of the McCullough-Pitts neuron, and that our brains are indeed made up of neurons of the type that McCullough and Pitts sought to model, it should come as no suprise that our internal view of the external world, both physical and spiritual, as a projection of, and reduction of basis of, the information space of that external world onto our internal consciousness, and being wholly contained in it, is also affected by, and reflected in, an apparent reciprocal internal projection of that underlying cuboctahedral structure upon the world as we see it, for indeed, we can only see it in our minds. |
|